How Quaternary is useful in determination of target location in 3D computer games?

Question

plz elaborate the concept of Axis of rotation and the Rotation Angle used in java3d to determine the shooting target in java3d games.
Is these two combined together (Axis of rot and Angle.rot) in vector form and called Quaternions.

loto app · Answer

The world of online gambling has become increasingly popular in India keno, with players able to access a wide variety of games and experiences that cater to their preferences. However, it is important for players to select a trustworthy and reputable online casino before diving in.

When choosing an online casino, it is essential to consider payment options, game selection, and security measures. Players should research different platforms and read reviews from other players to make an informed decision. This ensures that the platform chosen is reliable and provides a safe and enjoyable gambling experience.

Once players have selected a platform, they can create an account and make a deposit using a range of payment methods. The registration process is typically simple and requires basic information such as the player's name and email address.

One of the unique features of online casinos in India is the use of advanced technology, such as Random Number Generators (RNGs), which ensure that the outcome of each game is entirely based on chance. This level of transparency means that every player has an equal chance of winning and adds to the authenticity of the games.

Live dealer games are also a popular feature of online casinos in India, providing players with a realistic and immersive gambling experience. Hosted by professional dealers and streamed live to players, these games allow players to interact with the dealers and other players through a chat feature, adding to the social aspect of the game.

Online casinos in India often provide a range of bonuses and promotions to keep players engaged and motivated. These may include welcome bonuses, free spins, or loyalty programs, providing players with the opportunity to win more and explore new games without risking their own money. However, it is important to read the terms and conditions of these bonuses carefully, as they may come with restrictions or requirements.

Withdrawals at online casinos in India are usually quick and secure, with various payment options available. Players can use e-wallets, bank transfers, or credit cards to withdraw their winnings. Moreover, many platforms provide customer support in local languages, making it easier for players to get assistance whenever they need it.

In summary, online casinos in India offer a convenient and exciting way for players to gamble, with their vast selection of games, secure payment options, and advanced technology. As the online gambling industry continues to grow, players can expect even more innovative games and features to be added to these platforms, providing an even more compelling option for players seeking entertainment and thrills.

مستخدم محذوف‎ · Answer

The quaternions define a3d space with one additional dimention called axis of rotation.

Thus with little geometry giving Axis of rotation and degree of rotation .

Thus it help shooting an intercept in3d games.

formula for the quaternions,

q=q0+q1i+q2j+q3k= (q0, q1, q2, q3) q=q0+q where q0 is the scalar part and q is the vector part. formula for the quaternions,

i2 = j2 = k2 = ijk = −1,

Multiplication of basis elements

The identities

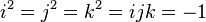$i^2=j^2=k^2=ijk=-1$ ,

where i, j, and k are basis elements of H, determine all the possible products of i, j, and k.

For example right-multiplying both sides of −1 = ijk by k gives

$\begin{align} -k & = i j k k = i j (k^2) = i j (-1), \\ k & = i j. \end{align}$

All the other possible products can be determined by similar methods, resulting in

$\begin{alignat}{2} ij & = k, & \qquad ji & = -k, \\ jk & = i, & kj & = -i, \\ ki & = j, & ik & = -j, \end{alignat}$

Using the basis1, i, j, k of H makes it possible to write H as a set of quadruples:

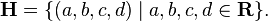
$\mathbf{H} = \{(a, b, c, d) \mid a, b, c, d \in \mathbf{R}\}.$

Then the basis elements are:

$\begin{align}1 & = (1,0,0,0), \\ i & = (0,1,0,0), \\ j & = (0,0,1,0), \\ k & = (0,0,0,1), \end{align}$

and the formulas for addition and multiplication are:

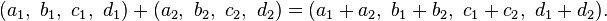
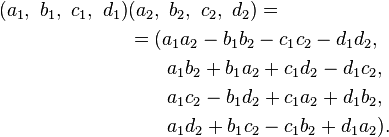
$(a_1,\ b_1,\ c_1,\ d_1) + (a_2,\ b_2,\ c_2,\ d_2) = (a_1 + a_2,\ b_1 + b_2,\ c_1 + c_2,\ d_1 + d_2).$ $\begin{align} (a_1,\ b_1,\ c_1,\ d_1)&(a_2,\ b_2,\ c_2,\ d_2) = \\ & = (a_1a_2 - b_1b_2 - c_1c_2 - d_1d_2, \\ & {} \qquad a_1b_2 + b_1a_2 + c_1d_2 - d_1c_2, \\ & {} \qquad a_1c_2 - b_1d_2 + c_1a_2 + d_1b_2, \\ & {} \qquad a_1d_2 + b_1c_2 - c_1b_2 + d_1a_2). \end{align}$

If a quaternion is divided up into a scalar part and a vector part, i.e.

$q = (r,\ \vec{v}),\ q\in\mathbf{H},\ r\in\mathbf{R},\ \vec{v}\in\mathbf{R}^3$

then the formulas for addition and multiplication are:

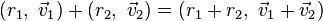
$(r_1,\ \vec{v}_1) + (r_2,\ \vec{v}_2) = (r_1 + r_2,\ \vec{v}_1+\vec{v}_2)$ $(r_1,\ \vec{v}_1) (r_2,\ \vec{v}_2) = (r_1 r_2 - \vec{v}_1\cdot\vec{v}_2, r_1\vec{v}_2+r_2\vec{v}_1 + \vec{v}_1\times\vec{v}_2)$

where "·" is the dot product and "×" is the cross product.

the conjugation of a quaternion can be expressed entirely with multiplication and addition:

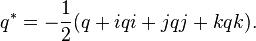
$q^* = - \frac12 (q + iqi + jqj + kqk).$

Conjugation can be used to extract the scalar and vector parts of a quaternion. The scalar part of p is (p + p*)/2, and the vector part of p is (p − p*)/2.

The square root of the product of a quaternion with its conjugate is called its norm and is denoted ||q|| (Hamilton called this quantity the tensor of q, but this conflicts with modern meaning of "tensor"). In formula, this is expressed as follows:

$\lVert q \rVert = \sqrt{qq^*} = \sqrt{q^*q} = \sqrt{a^2 + b^2 + c^2 + d^2}$

This is always a non-negative real number, and it is the same as the Euclidean norm on H considered as the vector space R4. Multiplying a quaternion by a real number scales its norm by the absolute value of the number. That is, if α is real, then

$\lVert\alpha q\rVert = |\alpha|\lVert q\rVert.$

This is a special case of the fact that the norm is multiplicative, meaning that

$\lVert pq \rVert = \lVert p \rVert\lVert q \rVert.$

for any two quaternions p and q. Multiplicativity is a consequence of the formula for the conjugate of a product. Alternatively it follows from the identity

$\det \Bigl(\begin{array}{cc} a+ib & id+c \\ id-c & a-ib \end{array}\Bigr) = a^2 + b^2 + c^2 + d^2,$

(where i denotes the usual imaginary unit) and hence from the multiplicative property of determinants of square matrices.

This norm makes it possible to define the distance d(p, q) between p and q as the norm of their difference:

$d(p, q) = \lVert p - q \rVert.$ This makes H into a metric space. Addition and multiplication are continuous in the metric topology

A unit quaternion is a quaternion of norm one. Dividing a non-zero quaternion q by its norm produces a unit quaternion Uq called the versor of q:

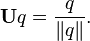
$\mathbf{U}q = \frac{q}{\lVert q\rVert}.$

Every quaternion has a polar decomposition q = ||q|| Uq.

Using conjugation and the norm makes it possible to define the reciprocal of a quaternion. The product of a quaternion with its reciprocal should equal1, and the considerations above imply that the product of q and q*/||q||2 (in either order) is1. So the reciprocal of q is defined to be

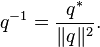$q^{-1} = \frac{q^*}{\lVert q\rVert^2}.$ Thus a quaternions is a3d vector with addition of one additional dimension to facilitate the Axis og rotation.

خدمات بيت.كوم

استخدم تطبيق بيت.كوم

ابدأ بالتواصل مع الأشخاص وتبادل معارفك المهنية

How Quaternary is useful in determination of target location in 3D computer games?

Multiplication of basis elements

عمليات البحث الشائعة

المزيد من الأسئلة المماثلة