What is special about number 1729?

Question

Hardy asked Ramanujan this question?

Tomasz Modrzejewski · Answer

Number of taxi - in mathematics, enta number of taxis, usually denoted Ta (n) or Taxicab (n), is defined as the smallest number that can be expressed as the sum of two cubes in the n different ways. GH Hardy and EM Wright proved in1954 that such numbers exist for all positive integers n. However, the evidence does not help in determining the consecutive numbers Ta (n). So far known taxi twelve consecutive numbers.

$\\operatorname{Ta}(1) =2 =1^3 +1^3$

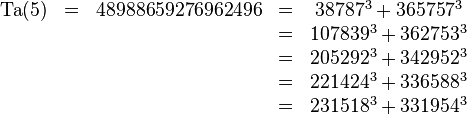
$\\begin{matrix}\\operatorname{Ta}(2)&=&1729&=&1^3 +12^3 \\\\&&&=&9^3 +10^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(3)&=&&=&167^3 +436^3 \\\\&&&=&228^3 +423^3 \\\\&&&=&255^3 +414^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(4)&=&&=&2421^3 +19083^3 \\\\&&&=&5436^3 +18948^3 \\\\&&&=&10200^3 +18072^3 \\\\&&&=&13322^3 +16630^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(5)&=&6&=&38787^3 +365757^3 \\\\&&&=&107839^3 +362753^3 \\\\&&&=&205292^3 +342952^3 \\\\&&&=&221424^3 +336588^3 \\\\&&&=&231518^3 +331954^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(6)&=&2065344&=&582162^3 +^3 \\\\&&&=&3064173^3 +^3 \\\\&&&=&8519281^3 +^3 \\\\&&&=&^3 +^3 \\\\&&&=&^3 +^3 \\\\&&&=&^3 +^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(7)&=&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3\\\\&&&=&^3 +^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(8)&=&352&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3\\\\&&&=&^3 ^3\\\\&&&=&^3 ^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(9)&=&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3 \\\\&&&=&^3 ^3\\\\&&&=&^3 ^3\\\\&&&=&^3 ^3\\\\&&&=&^3 ^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(10)&=&4&=&8^3 ^3 \\\\&&&=&6^3 ^3 \\\\&&&=&2^3 ^3 \\\\&&&=&8^3 ^3 \\\\&&&=&7^3 ^3 \\\\&&&=&8^3 ^3\\\\&&&=&3^3 ^3\\\\&&&=&2^3 ^3\\\\&&&=&0^3 ^3\\\\&&&=&6^3 ^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(11)&=&&=&4056^3356^3 \\\\&&&=&3042^314^3 \\\\&&&=&9724^352^3 \\\\&&&=&0696^316^3 \\\\&&&=&2786^326^3 \\\\&&&=&3769^347^3\\\\&&&=&2476^336^3\\\\&&&=&3461^351^3\\\\&&&=&3824^352^3\\\\&&&=&7120^38^3\\\\&&&=&1122^34^3\\end{matrix}$ $\\begin{matrix}\\operatorname{Ta}(12)&=&5152&=&7910376^3124676^3 \\\\&&&=&9077782^3271194^3\\\\&&&=&4540004^3611792^3 \\\\&&&=&1117816^3868036^3 \\\\&&&=&1107206^3397546^3 \\\\&&&=&3117699^3690237^3 \\\\&&&=&1936196^324056^3 \\\\&&&=&1112631^366121^3 \\\\&&&=&8071104^305892^3 \\\\&&&=&3143520^322628^3 \\\\&&&=&9476526^341026^3 \\\\&&&=&6363462^37674^3\\end{matrix}$

Fawzi Abusalma · Answer

it is the smallest number that can be written as the sum of cubes in two different ways.

9^3 +10^3 =1729
1^3 +12^3 =1729

They say that Ramanujan was in the hospital when he answered that, and immediately after hearing the number. that man is a great mathematician.

Vinod Jetley · Answer

The way I heard the story was that Hardy & Ramanujan were travelling in a car. Hardy saw the number of taxi in front of their car as1729, and he asked its significance from Ramanujan. Ramanujan replied within seconds that this is the smallest number which can be expressed as sum of cubes of two natural numbers in two different ways.

May be that is why Hardy later called them Taxi numbers.

Asmaa Mahmoud · Answer

Interesting question with interesting answer,it's a new information for me

Products By Bayt.com

Use Our Mobile App

Start networking and exchanging professional insights

What is special about number 1729?

Popular Searches

More Questions Like This